Zero-Knowledge Proofs I: Intro

Consider a login page. To log into your account, you typically provide a username, to identify yourself, and a password, a secret that confirms that you are who you say. Assuming you are actually the person in question (and have not forgotten your password), it is trivial to prove that you know your password. You just type it in. This is required because platforms do not trust that you are who you say without proof.
But what if you don't trust the platform? What if you don't want the platform to know your password? The problem becomes much more tricky, and this is the sort of question that zero-knowledge proofs are used to answer.
In abstract, a zk-proof is an approach used to prove exactly that something is true, without providing any other information. In cryptocurrency adjacent applications, "zk-proof" often refers to a specific type of such proofs, zero-knowledge proofs of knowledge.
A zero-knowledge proof of knowledge is a method to prove knowledge of some secret information, without revealing the information (even to the party requesting the proof). The person with the secret information is typically called the prover, and the party requesting the proof is typically called the verifier.
The limitations make examples a bit harder to construct, but thanks to the paper How to Explain Zero-Knowledge Protocols to Your Children by Jean-Jacques Quisquater et al., we have a canonical example handy:
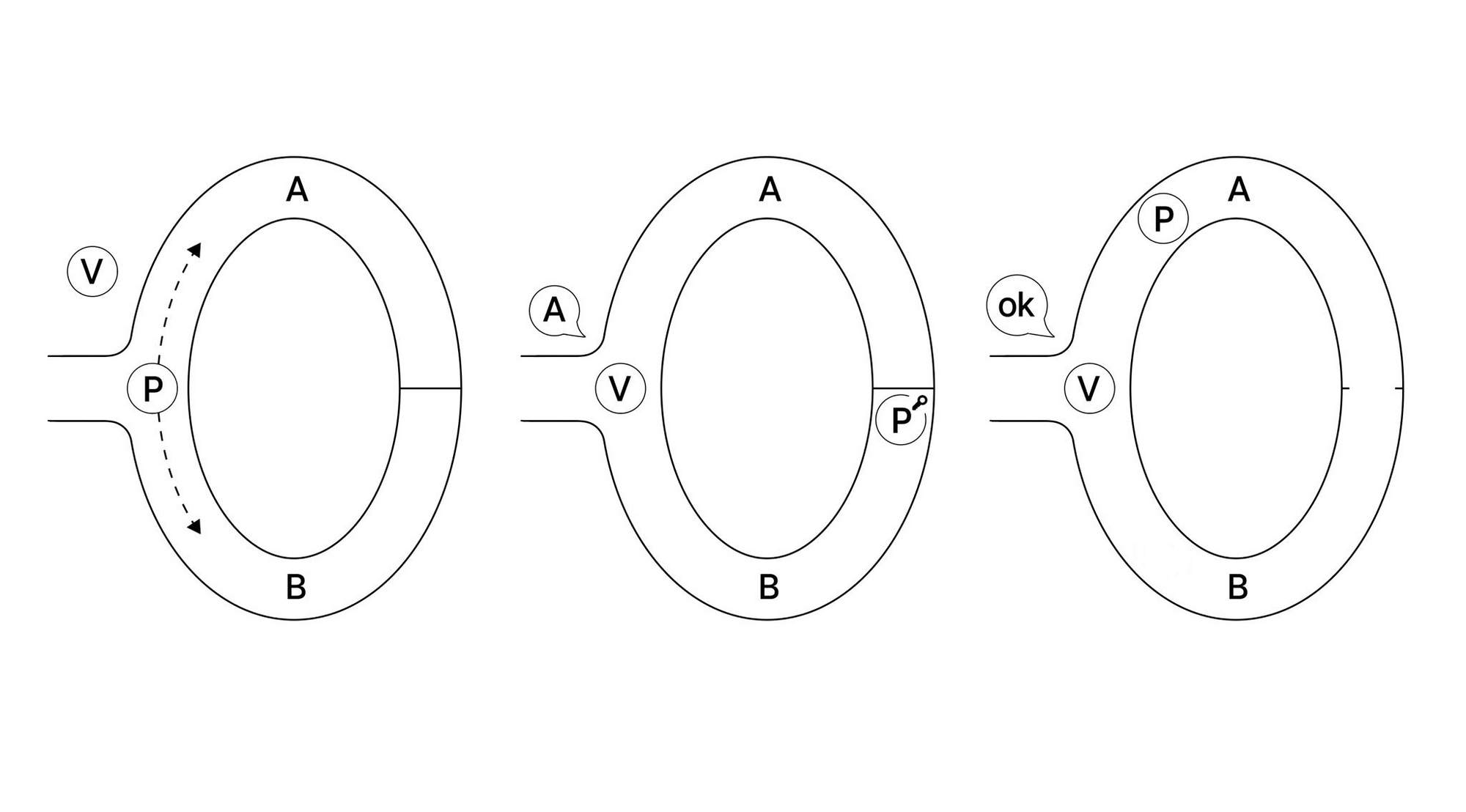
In this example, there is a cave containing a loop that is interrupted by a locked door. The prover (P) aims to prove that they have the key to this door. P enters the cave, and the verifier (V) cannot see into the cave. P chooses one of two paths to take, and arrives at a locked door at the other side of the cave. V cannot see which side of the cave P chose. V then enters the cave, and shouts to P that P should exit the cave from one of the two paths.
The first time P comes out on the correct side, there is only a 50% chance that they actually have the key... but the challenge can be repeated to V's satisfaction, with each iteration increasing confidence. If, for example, P comes out on the right side 100 times, there is only about a 0.000000000000000000000000000079% chance that P does not have the key.
Zero-knowledge proofs must be complete, i.e. the prover must be able to convince the verifier, assuming the prover and verifier are honest. Zero-knowledge proofs must be sound, i.e. a prover has at most some negligible probability of convincing the verifier if the prover is NOT being honest. Finally, zero-knowledge proofs must be zero-knowledge, i.e. the verifier does not learn anything other than that the statement is true.
The last criteria is the distinguishing bit, and why zk-proofs are such a hassle. It also demands that zero-knowledge proofs are probabilistic, i.e. in the cave example, it's technically possible that the prover could just guess which side the verifier will ask for, (in practice the verifier would ask so many times that this possibility is negligible). This provides an additional bit of information from leaking: if someone else were to observe the interaction, they cannot be sure that the prover knows the secret, because the prover and verifier could have agreed to a sequence beforehand, precisely to trick such observers.
In our next article, we'll take a look at some more crypto-specific applications of zk-proofs, and discuss their role in Web3 development.
Probabilistic algorithms may seem unintuitive, but are used practically in many other applications, two popular primality tests for example.